Hey All,
To preface this, I know the calculations on how to figure out size at a distance and things of that nature. I am pretty confident on how to use my mil-dot for calculations.
And Granted there are huge factors that play a role when you increase distance but this would be a pure exercise in target size in the scope. And getting comfortable with it.
However, And I may be biting off more than I can chew here, but I have a pretty big math question for you. I have heard rumors about elite units shooting the tops off of match sticks at a very close distance and that representing a head shot at a very lengthy distance.
I want to know how to make smaller targets to shoot at closer distances that represent normal targets at further distances.
How do I do that?
Example:
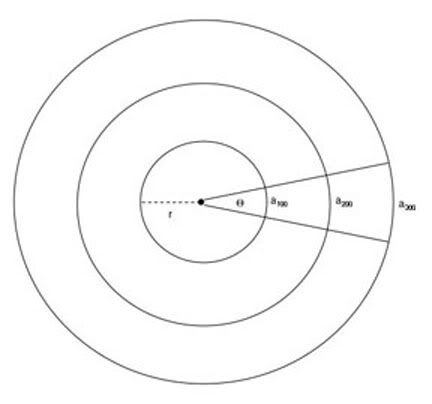
Lets say my intended target is 11". At 100 yards that 11" will appear as (A) big. At 10 yards I can make my target (B) to appear as (A) which will duplicate those 11" at 100 yards.
I hope I am getting my point across and that somebody may have some type of math for that?
A buddy of mine came up with this. What do you guys think?
<span style="font-style: italic">Ok, so quick response because we've been discussing this for the last 20 minutes or so, but I wanted this posted so that someone could check my math.
Using the formula:
For distance in yards: (27.77 X Target Dimension) ÷ Mil Reading = Range
we found here, I solved for mil for a 11" x 8" target @ 100 yards = 3 x 2.2
Using those mil numbers, I solved for target dimension based on 10 yard range, and came up with 1" by .8" to "fill" the same mil readings as the original 11" x 8" target @ 100 yards.
Can someone spot check my math and/or confirm I'm even using a correct forumla?
</span>
To preface this, I know the calculations on how to figure out size at a distance and things of that nature. I am pretty confident on how to use my mil-dot for calculations.
And Granted there are huge factors that play a role when you increase distance but this would be a pure exercise in target size in the scope. And getting comfortable with it.
However, And I may be biting off more than I can chew here, but I have a pretty big math question for you. I have heard rumors about elite units shooting the tops off of match sticks at a very close distance and that representing a head shot at a very lengthy distance.
I want to know how to make smaller targets to shoot at closer distances that represent normal targets at further distances.
How do I do that?
Example:
Lets say my intended target is 11". At 100 yards that 11" will appear as (A) big. At 10 yards I can make my target (B) to appear as (A) which will duplicate those 11" at 100 yards.
I hope I am getting my point across and that somebody may have some type of math for that?
A buddy of mine came up with this. What do you guys think?
<span style="font-style: italic">Ok, so quick response because we've been discussing this for the last 20 minutes or so, but I wanted this posted so that someone could check my math.
Using the formula:
For distance in yards: (27.77 X Target Dimension) ÷ Mil Reading = Range
we found here, I solved for mil for a 11" x 8" target @ 100 yards = 3 x 2.2
Using those mil numbers, I solved for target dimension based on 10 yard range, and came up with 1" by .8" to "fill" the same mil readings as the original 11" x 8" target @ 100 yards.
Can someone spot check my math and/or confirm I'm even using a correct forumla?
</span>