It’s voodoo.
Algorithms utilize our input parameters and spit out numbers representing ballistic come-up. That is, AFTER the algorithm bounces our bullet’s performance characteristics off the atmospherics conditions provided by link-up to Bluetooth devices that use other algorithms to spit out numbers representing atmospheric condition. Absolute voodoo I tell you. No way to figure this stuff out without known D.O.P.E. Or a drop solution produced by a complicated algorithm. Just no way.
That’s all great when I’m dealing with my known rifle, utilizing my known load, and my known fundamentals, which have been polished by tens of years of development and discipline and removing any influence I may contribute to an errant flight of that bullet. But I’m an instructor, on a line full of wide-eyed students, all awaiting my recommendation for data to put on the rifle in order to get a hit on the next target at the next 100-yard increment while gathering “try DOPE”. I need the answer. They are looking to me for the answer and it needs to be closer to right.
I can spit out a generic come-up and hope for the best, but am I really doing the student a service, limiting his percentage for a miss and not driving up his round count? I’m a professional. I must do better than that.

I need to dig into what is really going on… deep into the voodoo, and find a better, more predictable solution for that student, without having to chrono his rifle and pull up B.C. Data from a written or online resource. For each student in a 16-student class that takes time — Valuable time that I am being paid for on a firing line.
So that is just what I did.
Students generally bring one of only six or eight ballistic profiles to a course; slow .308 Win., fast .308 Win., slow 6.5, fast 6.5, the occasional 7 SAUM or WSM or the lightning bolt of a long-action .30 cal. In our Alaska Course, this may include .270, .243, .338 Win. Mag. and even .30-.378. There is about an even split between hunters and tactical shooters in Alaska, so Frank and I have to be ready for near anything. Alaska shooters are also not overly dependent on data acquired from smart phones because they don’t work when cold. Hard data is more preferred, especially among the hunters. Regardless of cartridge, they all have a very common characteristic: The percentage of drop utilized between each 100-yard increment. We teach on a 1,000-yard range, so most everyone except the “shortys” and “gassers” with 168 SMKs are still super-sonic and will be predictable and repeatable at 1,000 yards.
At our Alaska Precision Rifle Course, we had a real struggle that was costing us valuable time. A dip in terrain at the 900-yard line required us to get our 900-yard target high in the air in order for the student to see it clearly for a shot. The problem that presented to the instructor is that our call, being generic, did not close the danger space tight enough to assure a near-center plate hit on the first or second shot. And the dip in terrain made a splash, which appeared to miss low, but was actually a miss high that impacts seventy or so yards beyond, but was viewed under the target! And a miss low fell into dead space where we could see no impact!

Weaponizing the Math
We had to skip the 900 and go to the 1,000, then back into the 900. But I’m better than that. After all, I’ve got a high school education from central Mississippi, the finest the nation has to offer.
We, as instructors, simply had to get better at our predictable calls. For our professional sakes and for our reputation’s sakes.
So, I started thinking about the percentage of drop difference between 800 center-plate data and the 1,000 center-plate data. I “figured” that the bullet dropped 45% between the 8 and 900 and 55% between the 900 to 1,000 of the total drop of 100%. Just actually pulled that number out of the air. So I went back, way back, to simple-man Mississippi math, and worked out a formula to get that magic 900-yard data call, regardless of ballistic profile or rifle.
It went like this:
1,000-yard data MINUS 800-yard data EQUALS a number. That number represents the drop between 800 and 1,000, in Mils or MOA. Take that number and multiply it by .45 and it would give me the 45% drop between 800 and 900 that I was looking for… AND IT DID… ALMOST EVERY TIME.
Student influence on bullet travel is still in it, so it did not work out perfectly EVERY time, but boy, was it a time and ammo saver!
Take my 6.5, for instance, at my home range: 8.7 at 1,000 minus 5.8 at 800 equals 2.9 Mils of drop in that 200-yard gap. If I take that 2.9 and multiply it by .45, it gives me 1.3 Mils. Add that to my 800-yard data of 5.8 and it gives me… guess what…? What my TRASOL spits out for my 900-yard data!
8.7-5.8 = 2.9.
2.9 x .45 = 1.3
5.8 + 1.3 = 7.1 Mils
7.1 Mils to a water-line hit
This was great. Problem solved at 900 from now on, and it saved student ammo and instructor aggravation. I could now concentrate on the student’s wind call knowing that the data I gave him was elevation-correct, minus his input and windage. And it works in MOA or Mil, of course. I had created voodoo.

But voodoo is addictive, like those gay seltzer sodas that give you just enough buzz to want something more, like whiskey. So I dove into the deep-voodoo whiskey and took it further.

I wanted predictable hits from the 300-yard line on. I wanted a formula that could allow me to predict, for the student, what the next
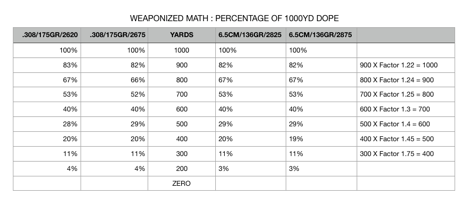
The drop percentages are remarkably similar. Remarkable Voodoo.
I reverse-engineer-math’d (copyrighting that term, thank you) the drops from 300 to 400, 400 to 500, and so on all the way out to 1,000. I found numeric values, “factors”, that when multiplied to the previous yardline’s KNOWN drop data could predict the following 100-yardline’s data. And guess what… THAT voodoo worked too.
Here’s what I found:
300 yard drop data X factor 1.75 = 400-yard data
400-yard drop data X factor 1.45 = 500-yard data
500-yard drop data X factor 1.40 = 600-yard data
600-yard drop data X factor 1.30 = 700-yard data
700-yard drop data X factor 1.25 = 800-yard data
800-yard drop data X factor 1.24 = 900-yard data
900-yard drop data X factor 1.22 = 1,000-yard data
Before you ask…I ran these numbers at 1,500 D.A., 4,500 D.A. And 7,500 D.A. The error was very slight, measured in only one or two tenths of Mils. Less than an MOA. A ballistic solver prediction is much more precise, but requires parameter input.
Hyper-Velocity cartridges have a smaller X-Factor, which can be calculated simply and predictably.
We are now calling hits on unknown student rifles using just the last yard-line’s drop data and the “X-factor.” (!!!) And students are now looking at us like we are voodoo witchdoctors. But that’s really all that’s in your ballistic solver —- VOODOO
Marc Taylor
Alaska Precision Rifle Course

