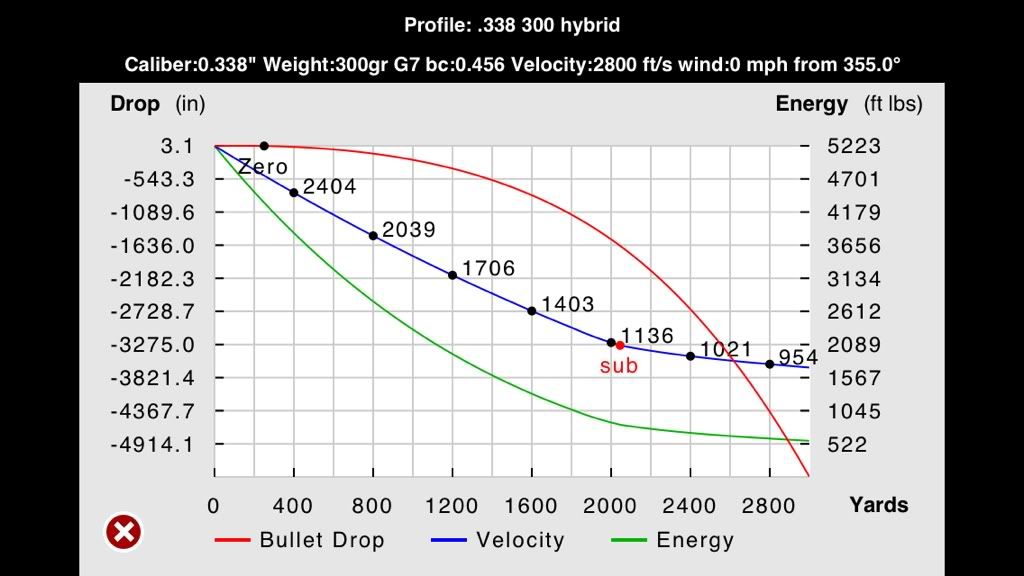
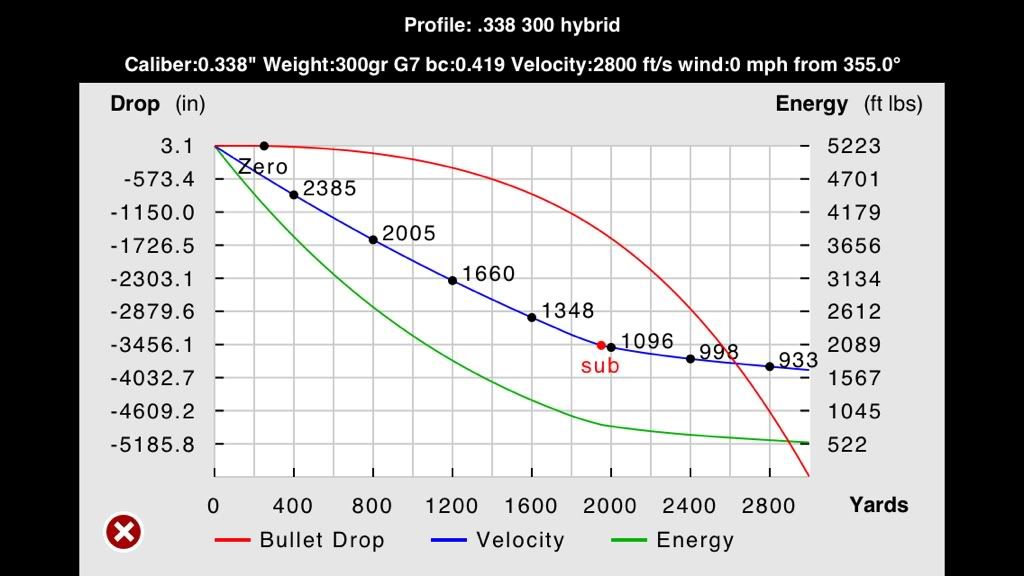
http://www.longrangehunting.com/articles/bullet-pitch-yaw-1.php
I thought the readers here might appreciate a link to a recent article.
Abstract
A bullet can leave the barrel with a significant yaw angle (or tip off rate leading to pitch and yaw) and then pitch and yaw in an oscillatory manner as the peak pitch and yaw angles slowly decrease as the bullet flies downrange. This paper presents an experimental design for detecting the in-flight damping and test results which support the theory of damping of pitch and yaw. Three chronographs were employed simultaneously to determine drag coefficients of bullets over near and far intervals 50 yards long for bullets fired at Mach 1.4 to Mach 3.1. Drag coefficients for the complete 100 yard interval were used at different Mach numbers to establish the curve of drag coefficient vs. Mach number. Since the drag coefficients will decrease as pitch and yaw are damped, the theory of bullets going to sleep predicts that the drag coefficients for the near 50 yard interval will be above the curve and the drag coefficients for the far 50 yard interval will be below the curve. This is, in fact, observed for Mach numbers above 1.5, so the theory of bullets going to sleep is supported in this case. Between Mach 1.0 and Mach 1.5, the damping of pitch and yaw may be obscured by the steep transonic drag rise.
I thought the readers here might appreciate a link to a recent article.
Abstract
A bullet can leave the barrel with a significant yaw angle (or tip off rate leading to pitch and yaw) and then pitch and yaw in an oscillatory manner as the peak pitch and yaw angles slowly decrease as the bullet flies downrange. This paper presents an experimental design for detecting the in-flight damping and test results which support the theory of damping of pitch and yaw. Three chronographs were employed simultaneously to determine drag coefficients of bullets over near and far intervals 50 yards long for bullets fired at Mach 1.4 to Mach 3.1. Drag coefficients for the complete 100 yard interval were used at different Mach numbers to establish the curve of drag coefficient vs. Mach number. Since the drag coefficients will decrease as pitch and yaw are damped, the theory of bullets going to sleep predicts that the drag coefficients for the near 50 yard interval will be above the curve and the drag coefficients for the far 50 yard interval will be below the curve. This is, in fact, observed for Mach numbers above 1.5, so the theory of bullets going to sleep is supported in this case. Between Mach 1.0 and Mach 1.5, the damping of pitch and yaw may be obscured by the steep transonic drag rise.